|
改進(jìn)蟻群算法在移動(dòng)機(jī)器人路徑規(guī)劃中的應(yīng)用研究
董武連 2021/8/7 20:34:08
(接上頁)er>
公式(5)中�, 代表起點(diǎn)螞蟻相遇時(shí)爬行的最短路徑, 代表終點(diǎn)螞蟻相遇時(shí)爬行的最短路徑��。
2.2.2 基于路徑選擇的算法改進(jìn)
依據(jù)蟻群算法原理���,螞蟻在爬行過程中路徑的選擇與信息素濃度大小密切相關(guān)��,可以將其理解為正反饋機(jī)制�����。如果螞蟻在爬行過程中在某條路徑中留下的信息素較多����,則接下來從起點(diǎn)出發(fā)的螞蟻選擇此路徑的概率就會(huì)隨之提升�����。從理論層面分析,這種路徑選擇方法雖然能夠?qū)崿F(xiàn)智能選擇���,但是嚴(yán)重限制了螞蟻爬行路徑����,縮小了選擇空間��,很有可能避開最優(yōu)爬行路徑��。為了彌補(bǔ)算法在路徑選擇方面的不足�,本文提出擴(kuò)大搜索范圍研究思想,在路徑選擇設(shè)置方面�,采取多樣性布設(shè),即利用信息素感應(yīng)進(jìn)行限定����。假設(shè)螞蟻對路徑中信息素最小感應(yīng)數(shù)值為 �,當(dāng),某條路徑的信息素低于 時(shí)�,則螞蟻感受不到這個(gè)信息素,將選擇其他路徑�。在此情況下,低信息素對螞蟻爬行路線的影響就會(huì)大大降低����,使得螞蟻選擇爬行的路徑范圍得以擴(kuò)大���。
隨著算法應(yīng)用時(shí)間的推移,各條路徑信息素逐漸增加��,當(dāng)其積累到一定程度后�,就會(huì)出現(xiàn)大于 的情況,此時(shí)信息素開始產(chǎn)生爬行路徑引導(dǎo)作用��。按照此路徑選擇方法�,可以將螞蟻在兩個(gè)城市之間的爬行路徑選擇概率用以下公式表示:
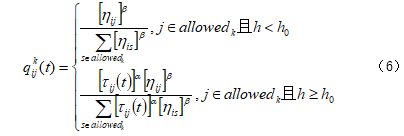
對于公式(6)閾值范圍以外的情況, �。
2.2.3 基于揮發(fā)系數(shù)調(diào)節(jié)的算法改進(jìn)
基于蟻群算法原理,算法性能容易受信息素發(fā)揮系數(shù)的影響����,該系數(shù)與螞蟻爬行路徑的引導(dǎo)存在負(fù)相關(guān)關(guān)系,如果系數(shù)數(shù)值較大���,則引導(dǎo)螞蟻選擇爬行路徑的作用就會(huì)減弱�,大大降低了螞蟻路徑選取的智能作用���。反之����,如果系數(shù)數(shù)值過小,則引導(dǎo)爬行路徑作用加強(qiáng)�,導(dǎo)致路徑搜索范圍減小。為了彌補(bǔ)蟻群算法在發(fā)揮系數(shù)方面的不足��,本文提出一種調(diào)整系數(shù)的方法���,在算法應(yīng)用初始階段����,適當(dāng)減小發(fā)揮系數(shù)數(shù)值�����,使得螞蟻爬行之間的引導(dǎo)得以下降���,達(dá)到擴(kuò)大搜索范圍的目的,此時(shí)路徑搜索效率會(huì)隨之提升�����。當(dāng)路徑搜索進(jìn)入后期時(shí)�,逐漸增加發(fā)揮系數(shù)數(shù)值,體現(xiàn)群智能選擇路徑性能,采用此方法快速收斂����,從而在短時(shí)間內(nèi)獲取最優(yōu)路徑。按照此優(yōu)化思路���,對發(fā)揮系數(shù)進(jìn)行調(diào)整�,計(jì)算公式如下:
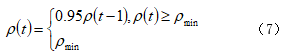
公式(7)中�, 代表發(fā)揮系數(shù),設(shè)定初始值為1��。該數(shù)值隨著算法應(yīng)用時(shí)間的推移�,系數(shù)數(shù)值逐漸減小,最終達(dá)到最小值���。
3 改進(jìn)蟻群算法在移動(dòng)機(jī)器人路徑規(guī)劃中的應(yīng)用
3.1 改進(jìn)算法的應(yīng)用
將上述提出的改進(jìn)蟻群算法應(yīng)用至移動(dòng)機(jī)器人行走路徑規(guī)劃當(dāng)中��,具體應(yīng)用流程如下:
第一步:對算法中所有參數(shù)采取初始化處理��。其中��,初始化參數(shù)包括 信息素感應(yīng)閾值�、 期望啟發(fā)因素�、 信息啟發(fā)因子等�����;第二步:等份分割螞蟻�,將兩部分相同數(shù)量的螞蟻分別放置起始點(diǎn)和終點(diǎn)����,自適應(yīng)調(diào)整發(fā)揮系數(shù),根據(jù)不同情況選擇爬行路徑���,直至兩組螞蟻在途徑相遇��;第三步:每一次遍歷后�����,更新信息素�;第四步:統(tǒng)計(jì)當(dāng)前算法循環(huán)次數(shù)���,如果該次數(shù)達(dá)到了上限����,則最后一次生成的最短路徑就是最優(yōu)路徑�,如果未達(dá)到上限,則返回第二步�。
3.2 仿真結(jié)果分析
為了檢驗(yàn)本文提出的改進(jìn)算法應(yīng)用方案可靠性,通過仿真模擬分析進(jìn)行檢驗(yàn)�����。該仿真實(shí)驗(yàn)以正方形區(qū)域路規(guī)劃為例����,要求機(jī)器人從左上角移動(dòng)到右下角,移動(dòng)期間避開障礙物�����。以傳統(tǒng)蟻群算法作為對照組���,以本文提出的改進(jìn)算法作為實(shí)驗(yàn)組�����,采用不同算法模擬機(jī)器人到達(dá)指定地點(diǎn)避開障礙物的行走路徑�����。其中�,機(jī)器人工作環(huán)境中的格柵大小為(20×20),最大迭代次數(shù)為300���,蟻群規(guī)模為30�。如圖1所示為兩種算法遍歷期間最大迭代次數(shù)仿真結(jié)果�,圖2為兩種算法螞蟻爬行路徑規(guī)劃結(jié)果。
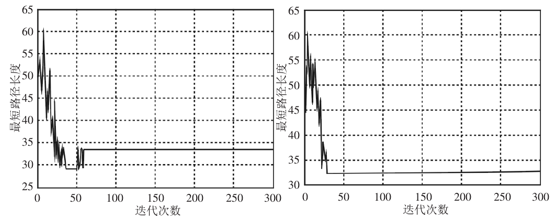
(a)傳統(tǒng)算法最大迭代次數(shù)變化曲線���;(b)改進(jìn)后的算法最大迭代次數(shù)變化曲線
圖1兩種算法遍歷期間最大迭代次數(shù)仿真結(jié)果
注釋:縱坐標(biāo)以格柵網(wǎng)格數(shù)量表示最短路徑長度�;橫坐標(biāo)為迭代次數(shù)���,單位:次�。
圖1中�,改進(jìn)后的算法找到最短路徑耗費(fèi)時(shí)間相對短一些,最大迭代次數(shù)大約30次�,而傳統(tǒng)算法的最大迭代次數(shù)超過了50次。所以���,改進(jìn)后的算法在收斂速度方面具有一定優(yōu)勢�����。

(a)傳統(tǒng)算法路徑規(guī)劃結(jié)果 (b)改進(jìn)后的算法路徑規(guī)劃結(jié)果
圖2兩種算法螞蟻爬行路徑規(guī)(未完�,下一頁)
|