|
初中數(shù)學(xué)教學(xué)中數(shù)形結(jié)合思想的應(yīng)用
葉 紅 2022/2/16 19:18:21
(接上頁)遇到諸多問題,此時(shí)教師便可通過數(shù)形結(jié)合方式對(duì)相關(guān)問題進(jìn)行講解���。首先�,教師可將一元二次方程比喻成一條拋物線�,并設(shè)置問題:一元二次方程公式為:y=ax2+bx+c。其中���,a并不等于0�����,求a、b�、c的正負(fù)���。隨后����,教師給出圖形(見圖4�、5)并讓學(xué)生結(jié)合圖形進(jìn)行思考����。當(dāng)學(xué)生完成解題后��,教師可作出解析:a點(diǎn)的正負(fù)片段主要取決于拋物線的開口方向����,若a>0�,表明開口向下�,而a<0,則代表拋物線開口向下�����,首先通過圖形可以看出拋物線開口向下���,因此得出a<0;b的正負(fù)主要取決于拋物線頂點(diǎn)處于第幾象限之中,若在第一象限當(dāng)中,則b>0���,若處于第四象限,便<0��,由圖形可知��,拋物線頂點(diǎn)在第一象限當(dāng)中,因此得出b>0�;而要判斷c的正負(fù)��,則完全可以將x=0完全帶入至拋物線方程y=ax2+bx+c當(dāng)中�,觀察(0,e)坐標(biāo)與y軸的交接點(diǎn)���,若y軸與正半軸相交��,則c>0���,反之,則c<0�����。由圖形可知�����,當(dāng)x=0時(shí)����,拋物線便是y=c���,此時(shí)y軸與a點(diǎn)相交,得出c>0����。由此可得出結(jié)論:a<0,b>0���,c>0�。

圖4 y=ax2+bx+c圖像(a>0) 圖5 y=ax2+bx+c圖像(a<0)
另外���,以勾股定理這一知識(shí)點(diǎn)為例�����,這一知識(shí)點(diǎn)一直是初中數(shù)學(xué)教學(xué)的難點(diǎn)��,教師若想有效降低學(xué)習(xí)難度,幫助學(xué)生更好地運(yùn)用勾股定理����,可通過多媒體將勾股定理圖直觀展示在學(xué)生眼前(見圖6),并在展示過程中對(duì)勾股定理如何形成進(jìn)行講解�,當(dāng)學(xué)生對(duì)勾股定理相關(guān)內(nèi)容形成一定了解后,教師便可使用不同圖形幫助學(xué)生有效論證勾股定理��,同時(shí)也可對(duì)《幾何原本》中的相關(guān)知識(shí)內(nèi)容進(jìn)行挑選利用�����,為學(xué)生進(jìn)行更多關(guān)于勾股定理如何運(yùn)用的講解��。這樣既能為學(xué)生認(rèn)知與理解勾股定理知識(shí)點(diǎn)提供有效幫助�����,又能夠令初中數(shù)學(xué)教學(xué)內(nèi)容得到大幅度拓展���,同時(shí)可以為學(xué)生在日后日常生活當(dāng)中靈活運(yùn)用勾股定理打下良好的基礎(chǔ)��。
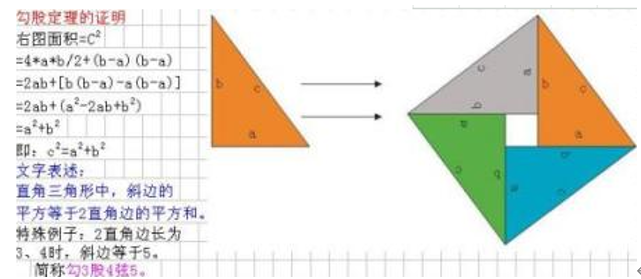
圖6 勾股定理證明圖
綜上所述�����,由于初中數(shù)學(xué)具有復(fù)雜��、抽象等特點(diǎn)���,大部分學(xué)生難以理解所學(xué)知識(shí)點(diǎn)����,對(duì)于這一問題��,教師可在初中數(shù)學(xué)課堂教學(xué)活動(dòng)當(dāng)中對(duì)數(shù)形結(jié)合思想進(jìn)行有效運(yùn)用���,因?yàn)閿?shù)形結(jié)合思想能幫助學(xué)生降低知識(shí)學(xué)習(xí)難度�����,并且對(duì)于促使學(xué)生形成數(shù)學(xué)素養(yǎng)也有著極為良好的促進(jìn)作用���。
參考文獻(xiàn):
[1] 郭禮軍.數(shù)形結(jié)合思想在初中數(shù)學(xué)教學(xué)中的應(yīng)用[J].數(shù)理化解題研究�����,2021�,(8).
[2] 王璠.初中數(shù)學(xué)教學(xué)中數(shù)形結(jié)合思想的應(yīng)用[J].讀寫算��,2021�,(7).
|