|
問題驅(qū)動(dòng)式教學(xué)法中問題設(shè)計(jì)的策略
資源天下 2024/3/5 8:18:47
(接上頁(yè))
再如在研究三角函數(shù)的誘導(dǎo)公式 和 之后,數(shù)學(xué)邏輯思維比較好的同學(xué)可以很快反應(yīng)出來(lái) �����,而思維一般的學(xué)生需要借助三角函數(shù)的定義和坐標(biāo)的關(guān)系進(jìn)行運(yùn)算�。因此合理設(shè)置問題情境必須要依照學(xué)生的自身實(shí)際,合理設(shè)置����。

四、問題驅(qū)動(dòng)式教學(xué)法問題設(shè)計(jì)的策略
基于問題設(shè)計(jì)的兩個(gè)要求——?jiǎng)?chuàng)設(shè)良好的教學(xué)情境��,設(shè)置合理的數(shù)學(xué)問題�,在具體設(shè)計(jì)教學(xué)問題時(shí)應(yīng)遵循以下策略���。
1����、問題設(shè)計(jì)具有情境性
弗賴登塔爾認(rèn)為:“數(shù)學(xué)教學(xué)應(yīng)該結(jié)合學(xué)生體驗(yàn)與數(shù)學(xué)現(xiàn)實(shí)”����,這里所指的學(xué)生體驗(yàn)和數(shù)學(xué)現(xiàn)是在問題設(shè)計(jì)時(shí),應(yīng)該考慮學(xué)生的實(shí)際���,符合前面所提及的設(shè)置合理問題情景的原則�����。問題的情境性指的是:在設(shè)置問題的過(guò)程中���,問題隱藏在情境中�,知識(shí)問題化����,問題情境化,情境現(xiàn)實(shí)化����,讓使得抽象的數(shù)學(xué)能夠和學(xué)生平常的生活相互契合,從而找到知識(shí)與學(xué)生的切入點(diǎn)�����,使得數(shù)學(xué)知識(shí)的抽象和思維難度符合學(xué)生目前的發(fā)展情況�����,并且使得大部分學(xué)生都能夠進(jìn)入到課堂的思考和學(xué)習(xí)中去�����。此外,高考的試題的命制方向�,有這樣一條:高考評(píng)價(jià)體系中所謂的“情境”即“問題情境”,這個(gè)問題情境往往是真實(shí)的問題情境����,需要在這樣的情境下完成一定的思維和思考任務(wù)。因此在平時(shí)的課堂學(xué)習(xí)和訓(xùn)練中���,要逐步培養(yǎng)學(xué)生在真在情境中分析問題的能力��。因此問題的設(shè)計(jì)應(yīng)該具有情境性�。
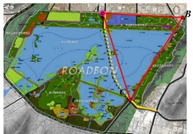
例如在學(xué)習(xí)完余弦定義之后可以這樣設(shè)計(jì)問題:如圖是云龍湖湖隧道設(shè)計(jì)示意圖���,工程人員要測(cè)量圖中 和 點(diǎn)的距離,請(qǐng)你設(shè)計(jì)如何測(cè)量更加便捷����。
云龍湖隧道是現(xiàn)實(shí)生活的情景,在設(shè)計(jì)隧道的真實(shí)情境下���,學(xué)生會(huì)思考用哪個(gè)定理比較容易進(jìn)行測(cè)量和計(jì)算��,在這個(gè)過(guò)程中��,學(xué)生也會(huì)對(duì)正弦定理和余弦定理進(jìn)行比較���,能夠根據(jù)問題中的不同信息選擇較為便捷的定理進(jìn)行求解���。在這個(gè)過(guò)程中,逐步培養(yǎng)起學(xué)生分析��、解決問題的能力�,并且提升學(xué)生的思維能力。
2��、問題設(shè)計(jì)具有拓展性
問題設(shè)計(jì)的拓展性是指問題相互之間是循序漸進(jìn)的���,難度逐步遞增的�����,它是在學(xué)生現(xiàn)有的基礎(chǔ)之上�����,提升學(xué)生的思維和認(rèn)知水平的�,要符合最近發(fā)展區(qū)的。具體體現(xiàn)在多題同解�����、一題多解���、一題多變等方面���。問題的拓展對(duì)于課堂教學(xué)的開展和學(xué)生思維的提高有著十分重要的意義,不僅可以豐富課堂中的學(xué)生活動(dòng)���,還可以在平時(shí)的數(shù)學(xué)教學(xué)中�����,不知不覺的提升學(xué)生分析問題����,解決問題���,處理問題的能力。
例如在復(fù)習(xí)函數(shù)的零點(diǎn)這一節(jié)內(nèi)容時(shí)可以設(shè)計(jì)如下問題串:
問題1:什么是函數(shù)的零點(diǎn)
概念:一般地�����,我們把使函數(shù) 的值為____的實(shí)數(shù)x稱為函數(shù) 的零點(diǎn).
問題2:函數(shù)的零點(diǎn)、函數(shù)的圖象與 軸的交點(diǎn)����、對(duì)應(yīng)方程的根有什么關(guān)系?

問題3:什么是零點(diǎn)存在性定理�����?
函數(shù)零點(diǎn)存在定理
(1)條件:①函數(shù) 在區(qū)間 上的圖象是一條不間斷的曲線�;
②____________________ .
(2)結(jié)論:函數(shù) 在區(qū)間 內(nèi)至少有一個(gè)零點(diǎn),即存在 �,使得______________,這個(gè) 也就是方程 的解.
思考:在下列情形中零點(diǎn)存在性定理還成立嗎
思考1 :如果 在區(qū)間 上的圖象是一條間斷的曲線���,零點(diǎn)存在性定理還成立嗎����?
思考2 :如果 在區(qū)間 上的圖象是一條不間斷的曲線��,零點(diǎn)存在性定理還成立嗎��?
思考3 :如果 在區(qū)間 上的圖象是一條單調(diào)且不間斷的曲線����,零點(diǎn)存在性定理還成立嗎��?
思考4如果 �,零點(diǎn)存在性定理還成立嗎����?
通過(guò)設(shè)置這3個(gè)問題以及4個(gè)思考,引導(dǎo)學(xué)生對(duì)于函數(shù)零點(diǎn)存在定理進(jìn)行思考����,循序漸進(jìn)。先是從函數(shù)零點(diǎn)的定義進(jìn)行復(fù)習(xí)入手�����,然后借助問題2學(xué)生思考函數(shù)零點(diǎn)的三個(gè)關(guān)系轉(zhuǎn)化���,最后再對(duì)函數(shù)的零點(diǎn)存在性定理的四個(gè)方面進(jìn)行思考�,逐步培養(yǎng)學(xué)生的分析問題能力���,在問題的逐步解決過(guò)程中達(dá)到有意義的數(shù)學(xué)建構(gòu)�。
3�����、問題設(shè)計(jì)具有啟發(fā)性
問題的設(shè)計(jì)應(yīng)能夠啟發(fā)學(xué)生思考��,激起學(xué)生探索的欲望���。學(xué)生是學(xué)習(xí)的主體����,學(xué)生能主動(dòng)進(jìn)行問題分析和思考是最先考慮的�����,而高中數(shù)學(xué)知識(shí)本身抽象概括程度高����,學(xué)生難以激起興趣,更無(wú)從下手思考���。合理的設(shè)置問題����,可以將復(fù)雜的知識(shí)����,抽象概括程度高的信息通過(guò)問題的形式呈現(xiàn)����,從而使得學(xué)生在解決一個(gè)又一個(gè)問題的基礎(chǔ)之上�����,逐步的獲取知識(shí)��,建構(gòu)自己的知識(shí)框架���,完善自己對(duì)于知識(shí)點(diǎn)(未完�,下一頁(yè))
附件下載:問題驅(qū)動(dòng)式教學(xué)法中問題設(shè)計(jì)的策略
|